三維空間機械臂的動力學建模與仿真分析
2017-3-10 來源:山東科技大學 機械電子工程學院 作者:吳良凱, 王濤, 王春麗, 王洲, 夏國
0 引 言
三維空間助力機械臂是一個復雜的動力學系統,它由多個關節和多個運動構件組成,各關節與運動構件之間存在復雜的耦合關系。為了機械臂的結構設計以及控制系統的開發與優化,對機械臂進行動力學分析與研究是非常重要的。越來越多設計人員將虛擬樣機仿真作為機械系統研發的重要依據,相比傳統機械設計而言,節省了物理樣機的實驗時間以及材料,縮短了設計周期,提高了機械臂工作性能。目前動力學分析領域中的方法主要包括拉格朗日法、牛頓-歐拉法、高斯方法、凱恩法、旋量法等,ADAMS是一款以計算多體動力學為基礎的虛擬樣機仿真分析軟件,可以對虛擬機械系統進行靜力學、運動學和動力學進行仿真計算;本文以四自由度空間助力機械臂為研究對象,用Solid Works建立機械臂的裝配體,運用拉格朗日方法對機械臂進行動力學建模,并用ADAMS進行動力學分析,為機械臂實際物理樣機的結構優化和控制研究提供依據。
1 機械臂組成部分及坐標系的建立
空間助力機械臂各個關節均為轉動連接,整個機構有底座、轉動平臺、平行臂、腕關節等組成。利用修正D-H法建立坐標系,三維空間助力機械臂的平面結構簡圖,如圖1所示。
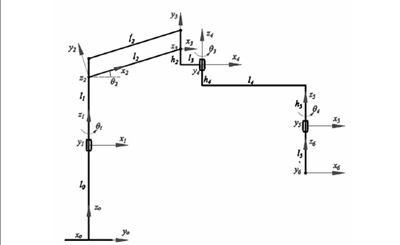
圖1 機械劈平面機構簡圖
2 動力學方程的建立
2.1 連桿質心位置的求解
各連桿參數通過坐標轉換可得到桿1-5質心在定坐標系O-X0Y0Z0下的坐標值如式(1)-式(5)所示:

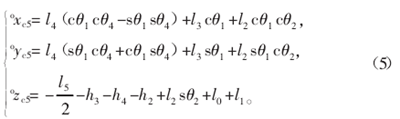
2.2 連桿動能和勢能的求解對質心坐標求導并代入動能公式,則各連桿動能為:
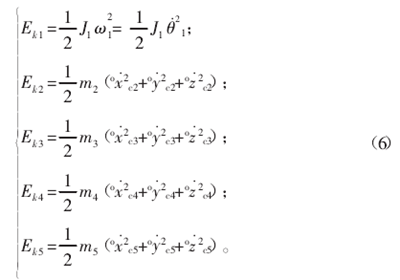
機械臂系統總動能為:Ek=Ek1+Ek2+Ek3+Ek4+Ek5。
假設地面為零勢能面,則各連桿勢能為:
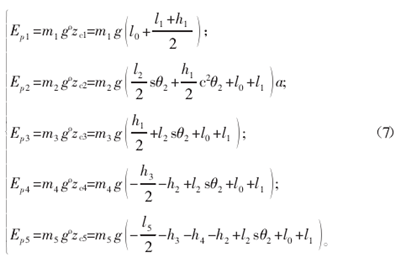
機械臂系統總勢能為:Ep=Ep1+Ep2+Ep3+Ep4+Ep5。
綜上,拉格朗日函數L為L=Ek—Ep。 (8)
2.3 系統動力學方程的建立
對式(8)求偏導數并帶入第二類拉格朗日動力學公式,得到關節1、2、4的力矩為:
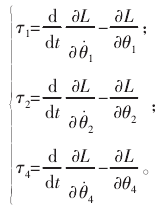
因關節3與關節2力矩大小相等,方向相反,故只計算關節2力矩即可,從而得到三維空間機械臂動力學方程為:
其中,

式中:D(q)為慣性矩陣,D(q)q為機械臂所受慣性力;H(q,q)為離心力與科氏力矩陣;G(q)為重力矩陣;τ為關節力矩矩陣。
3 ADAMS環境下動力學仿真
3.1 ADAMS動力學仿真環境設置
在Solid Works軟件中將裝配好的機械臂模型保存成與ADAMS的交互格式Parasolid,在ADAMS中,以實際物理樣機屬性為標準,對模型的各個構件進行編輯,賦予其材料、質量等屬性,便于仿真得到更加可靠的實驗結果。添加各運動副之間的約束和驅動,空間助力機械臂的ADAMS仿真模型如圖2所示。
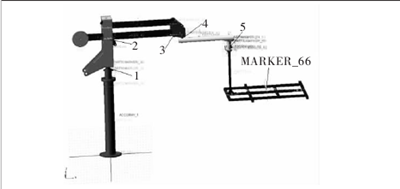
圖2 機械臂的ADAMS仿真模型圖
3.2 ADAMS動力學仿真
末端MARKER_66添加驅動函數如下:
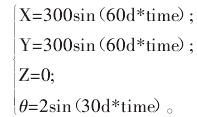
將驅動函數導入虛擬樣機的動力學模型中,利用ADAMS的測量功能,得到各轉動副關節驅動力矩的大小如圖3所示。
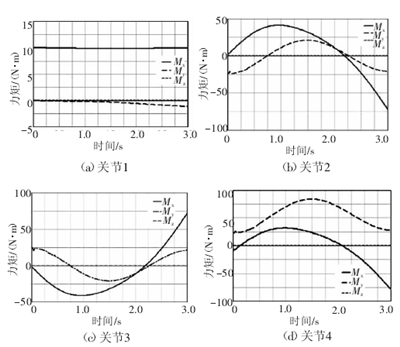
圖3 空間助力機械臂各關節力矩圖
4 結 語
對空間助力機械臂進行適當簡化,根據已知條件,運用拉格朗日方法建立空間助力機械臂的動力學理論模型,利用ADAMS進行動力學分析與研究,得到各個關節的力矩圖像,符合實際運動的要求,同時驗證了虛擬樣機仿真模型的合理性。為工業助力機械臂的結構設計和控制系統的開發與優化提供了依據,也為后續機械臂的動態特性及控制的研究打下基礎。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





