摘要: 機床有限元分析可以準確預測機床的性能,縮短機床研發周期,且龍門式銑床具有行程大、占地面積小等優點,因此龍門銑床的結構設計受到了廣泛關注。以微型移動龍門式銑床為研究對象,建立了其本體結構有限元模型,在具體工況下對其進行靜力學分析,得到了其應力、位移云圖和靜剛度; 通過模態分析,得到其前十階模態固有頻率和主振型。找到了機床的薄弱環節,為該銑床結構優化提供了依據。
關鍵詞: 微型銑床; 有限元; 靜力學; 模態分析
0 引言
在機床結構分析中,有限元分析是一種用于計算復雜結構且極為有效的數值分析方法,國內外學者在這方面做了大量的研究。Hung,Jui P. 等通過有限元仿真,研究了機床直線導軌在不同預載下對于整機動態特性的影響,驗證了該有限元模型對機床動態特性預測的可靠性[1]。Yu,Lianqing 等通過建立合理的結合面模型以及整機有限元模型,研究了機床整機剛度[2]。殊海燕等通過有限元軟件ANSYS 對數控立式機床做了靜力學和模態分析,找到了機床薄弱環節[3]。趙興玉利用有限元法對龍門銑床結構進行了靜動態分析,研究了各部件對整機剛度的貢獻,為其優化設計提供了理論依據[4]。
龍門銑床具有剛性好,效率高,操作方便,結構簡單,性能全面性等特點,且工作行程大,占地面積小,因此受到了廣泛關注。文章以微型移動龍門式銑床為研究對象,對其本體結構進行了靜動態特性的仿真,分析并找到了其結構中的薄弱環節,為該銑床的結構優化
提供了依據。
1 、微型銑床本體結構
該銑床床身材料采用45 鋼,其外形尺寸為900mm ×700mm × 655mm,工作行程為500mm × 400mm ×150mm,主軸轉速為0 ~ 15000r /min。其本體結構三維模型如圖1 所示。
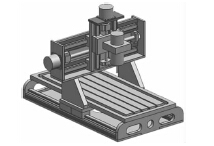
圖1 微型銑床本體結構
2 、機床模態分析理論
對于一臺機床,可將其看做一個多自由度的線性系統,其基本振動平衡方程為[5-7]:[ M] X··( ) { } t + [ ] C X· { ( t)}+ [ K]{X( t)}= {F( t)} ( 1)式( 1) 中: [ M] 為質量矩陣,[ C] 為阻尼矩陣,[ K] 為剛度矩陣, X··{ ( t) }、X· { ( t) }和{X( t) }分別為加速度向量、速度向量和位移向量,{F( t) }為載荷向量。取載荷向量{F( t) }為0 值,得到系統在無阻尼狀態下的自由振動方程:[ M] X··{ ( t)}+ [ K]{X( t)}= 0 ( 2)該銑床機構為彈性體,其自由振動可分解為一系列簡諧振動疊加,式( 2) 方程的解可寫為:{X( t)}= X0 { ( t)}sinωt ( 3)該銑床固有頻率和振型的求解也就是( 2) 式方程的求解,其解如式( 3) 所示。
3 、有限元模型的建立
3. 1 有限元網格的劃分
綜合考慮計算效率和精度,對該銑床幾何模型進行適當簡化,忽略進給電機及傳動系統對本體結構的影響,主軸電機作為剛體,去除螺紋孔和部分倒角等細小特征[8]。各部件之間的結合部采用ABAQUS 中連接單元TIE 模擬。采用八節點六面體單元對機床本體進行網格劃分,得到的有限元網格模型如圖2 所示。
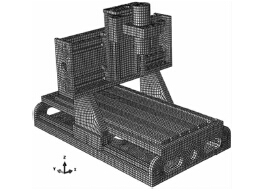
圖2 銑床本體有限元模型
3. 2 靜力學分析參數的確定
根據銑削力經驗公式有:

4 、結果與分析
4. 1 靜力學分析
在微型銑床刀具刀位點X、Y、Z 三個方向分別施加30. 6N 的力,同時在機床質點添加向下的重力加速度9800mm/s2,通過計算得到其靜剛度如表1 所示,其位移和應力云圖如圖3 所示。
表1 銑床位移和靜剛度

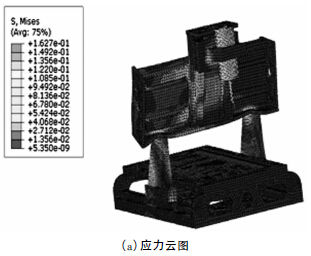

圖3 靜力學分析應力、位移云圖

4. 2 模態分析
采用ABAQUS 中的Lanczos 求解器提取了前10階模態頻率及其主振型,如表2 所示:
表2 微型銑床前十階振型表
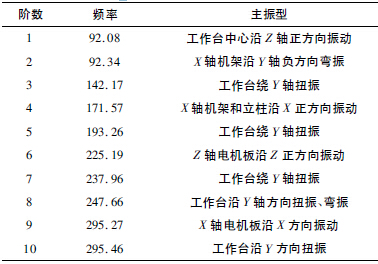
由于篇幅有限只給出了前四階振型圖如圖4 所示:

圖4 微型銑床前四階振型圖
由表2 和圖4 可知,機床前十階的固有頻率相差較大,機床整體有一定的抗震能力。工作臺的變形影響到工件在加工中的精確位置,為機床重要的結構部件,前十階的主振型有六階為工作臺的振動變形,且振動幅度相對較大,分析其原因為工作臺動剛度不足。另外,由于立柱以上的床身扭振,引起刀具的擺動較大,對銑削精度影響較大,分析其原因為立柱與X 軸連接部分尺寸較小,從而造成連接部位剛度不足[9-10]。因此需要增大工作臺本身的剛度以及立柱與X 軸床身連接部位的剛度,以求達到設計要求。
5 總結
文章通過對微型移動龍門式數控銑床進行靜力學和模態分析,分析了其靜剛度,找到了造成其結構剛度較弱的部位; 提取了其前十階的固有頻率和主振型,找到了其振動位移相對較大的部位,并分析了其原因,為該銑床進一步的結構分析和結構優化提供了參考依據。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com




