摘要: 數(shù)控磨床系統(tǒng)復雜性高,各子系統(tǒng)之間關聯(lián)性強。使用傳統(tǒng)的重要度分析方法難以進行分析。在對數(shù)控磨床進行可靠性建模的基礎上,獲得整機及子系統(tǒng)的可靠度函數(shù)。通過評分方式獲得各個子系統(tǒng)的關聯(lián)度,并使用蒙特卡洛仿真方法對數(shù)控磨床各子系統(tǒng)進行重要度綜合評價。此方法不僅考慮因素全面,而且在一定程度上減少了主觀性的影響。使用此方法對某批數(shù)控磨床進行重要度綜合評價結果表明該方法簡便,有效,實用性強。
0 引言
數(shù)控磨床是一種精密加工設備,其可靠性好壞是評價數(shù)控磨床好壞的一項重要評價指標。為了提升整機的可靠性水平,需要有針對性的對各個子系統(tǒng)進行可靠性提升。子系統(tǒng)重要度是評判子系統(tǒng)重要程度的一個指標。子系統(tǒng)越重要,越應該優(yōu)先提升該子系統(tǒng)的可靠性。因此,必須找到一種方法對系統(tǒng)進行更準確、更全面的重要度評價。系統(tǒng)的重要度評定方法有很多。曾亮等 在1998 年考慮了系統(tǒng)的多態(tài)性,提出了多狀態(tài)單調(diào)關聯(lián)系統(tǒng)元件重要度分析方法。孫紅梅等 在2007 年總結了基于故障樹進行重要度分析的方法。2009 年,李常有等 提出了基于改進的TOPSIS 設備重要度分析法,此方法采用信息熵法求權重并應用TOPSIS 方法得到重要度決策矩陣。姚成玉等 在2010 年提出了基于模糊理論的T-S 模糊故障樹重要度分析方法。以上文獻中所述的方法雖然能夠實現(xiàn)重要度評價,但都存在一定的缺陷。文獻 沒有考慮各個子系統(tǒng)的關聯(lián)性。文獻 對于重要度的評價主觀性過強。文獻 是基于故障樹的重要度分析方法,沒有建立完善的可靠性模型。
針對上述缺陷,本文提出一種利用歷史故障數(shù)據(jù)對系統(tǒng)與子系統(tǒng)進行可靠性建模,并考慮子系統(tǒng)之間的關聯(lián)性,同時運用蒙特卡洛仿真方法降低主觀性的重要度評價方法。應用此方法對數(shù)控磨床進行重要度分析,來驗證該方法的實用性。
1、 子系統(tǒng)劃分及可靠性建模
1. 1 子系統(tǒng)劃分
一個復雜系統(tǒng)由于功能多,結構復雜。在進行分析時,需要將其劃分為若干個子系統(tǒng)來降低復雜性。假設系統(tǒng)Ω,對其進行子系統(tǒng)劃分,其子系統(tǒng)集為Ri,Ri = ( 子系統(tǒng)1,子系統(tǒng)2,… ,子系統(tǒng)n ) 。
1. 2 可靠性建模
對系統(tǒng)進行可靠性建模,要找到可能符合的分布模型,再利用適當?shù)臄M合方法對其進行參數(shù)估計。最后驗證可靠性模型的有效性。由文獻 知,數(shù)控磨床可靠性模型符合指數(shù)分布或威布爾分布。
1. 2. 1 指數(shù)分布可靠性建模





1. 2. 3 可靠性分布擬合優(yōu)度檢驗及模型優(yōu)選K-S 檢驗法是對計算樣本數(shù)據(jù)的觀察值與擬合模型計算值求差。如果差小于允許值時,接受擬合模型;反之,不接受。

如果指數(shù)分布的相關指數(shù)R指數(shù)大于威布爾分布的相關指數(shù)R威布爾,則選取指數(shù)分布為可靠性模型的優(yōu)選分布模型; 反之,則選取威布爾分布為可靠性模型的優(yōu)選分布模型。
2 、臨界重要度指標
根據(jù)文獻 ,將臨界重要度重新定義為以下形式:

臨界重要度既考慮了整機系統(tǒng)可靠度隨子系統(tǒng)可靠度變化的變化率,又考慮了子系統(tǒng)本身可靠度大小的程度。如果整機系統(tǒng)可靠度因某一子系統(tǒng)可靠度變化而變化的變化率比較大,說明提高這一子系統(tǒng)的可靠度會使整機可靠度得到更大的提升。如果子系統(tǒng)的可靠度越低,說明能夠提升的潛力就越大。從這兩方面綜合考慮,能夠更全面的評價子系統(tǒng)的重要度。
3 、子系統(tǒng)關聯(lián)度
各個子系統(tǒng)相互聯(lián)系,相互作用,共同影響整個系統(tǒng)的狀態(tài)。采用專家評價的方式來得到子系統(tǒng)的關聯(lián)度。子系統(tǒng)評分取值區(qū)間在0 ~ 1 之間,越靠近0 表示影響越微小,越靠近1 表示影響越嚴重。得到評分值后,建立與之對應的子系統(tǒng)關聯(lián)度矩陣。


4 、基于蒙特卡洛方法的重要度評價
定義新的重要度評價指標為:
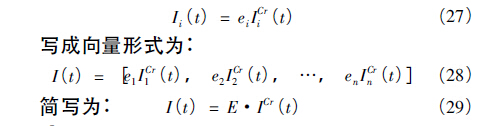

5 、應用實例
以北京第二機床廠某批9 臺數(shù)控磨床為例進行綜合重要度評價。對數(shù)控磨床進行子系統(tǒng)劃分,并按照上述方法進行可靠性建模,結果見表1。
表1 子系統(tǒng)代號和可靠度函數(shù)表
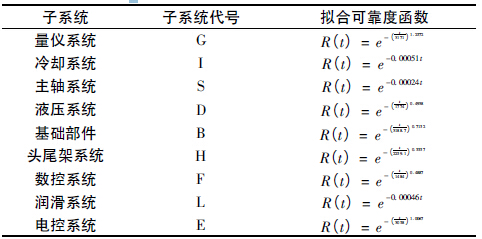


由式( 33) 計算出各個子系統(tǒng)的臨界重要度表達式。子系統(tǒng)的臨界重要度表達式為:
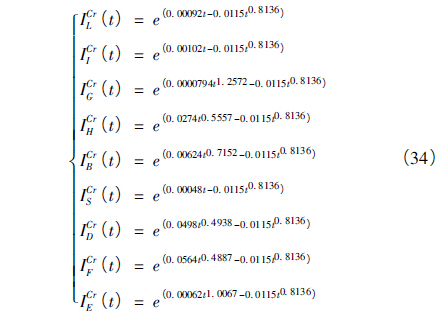
對子系統(tǒng)進行關聯(lián)度打分,結果見表2。
表2 子系統(tǒng)關聯(lián)度打分表
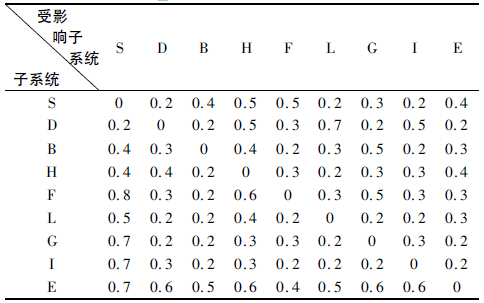
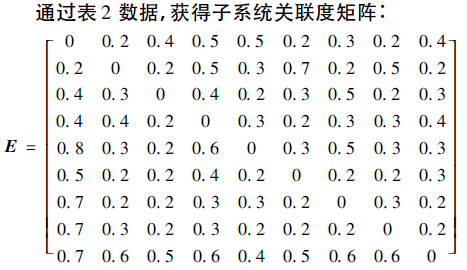

從結果可以得到子系統(tǒng)關聯(lián)度大小的排序: 電控系統(tǒng)> 數(shù)控系統(tǒng)> 液壓系統(tǒng)> 主軸系統(tǒng)> 基礎部件>頭( 尾) 架系統(tǒng)> 量儀系統(tǒng)> 冷卻系統(tǒng)> 潤滑系統(tǒng)。基于蒙特卡洛方法,使用Matlab 軟件進行蒙特卡洛仿真模擬,仿真的循環(huán)次數(shù)N = 150。
程序流程圖如圖1 所示。
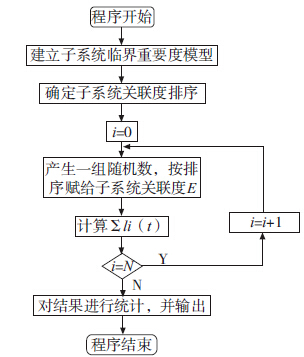
圖1 蒙特卡洛程序流程圖
每次循環(huán)產(chǎn)生一組隨機數(shù),將隨機數(shù)按大小順序賦給對應的子系統(tǒng)作為關聯(lián)度,進而按照式( 28) 計算出綜合重要度,對其進行累加,得到累積重要度。對累積重要度進行數(shù)據(jù)擬合,擬合曲線如圖2 所示。
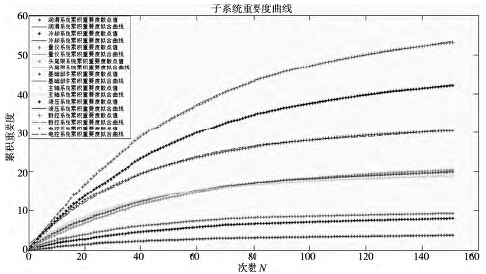
圖2 子系統(tǒng)累積重要度擬合曲線
累積重要度的三次多項式擬合表達式及其導數(shù)列于表3 中。
表3 累積重要度擬合多項式及其導數(shù)
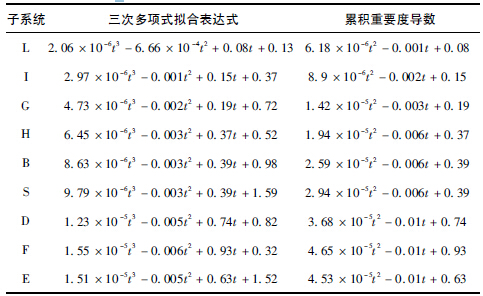

將歸一化后的累積重要度作為評價數(shù)控磨床各個子系統(tǒng)重要度的指標。
最后,得到的子系統(tǒng)重要度的先后排序為: 數(shù)控系統(tǒng)> 液壓系統(tǒng)> 電控系統(tǒng)> 頭( 尾) 架系統(tǒng)> 基礎部件> 主軸系統(tǒng)> 量儀系統(tǒng)> 冷卻系統(tǒng)> 潤滑系統(tǒng)。
數(shù)控系統(tǒng)、液壓系統(tǒng)和電控系統(tǒng)重要度排在前三位。其中電控系統(tǒng)的電子元器件較多,故障頻發(fā),關聯(lián)度排在第一; 數(shù)控系統(tǒng)時常出現(xiàn)數(shù)控指令不能正常運行的情況,關聯(lián)度排在第二; 液壓系統(tǒng)出現(xiàn)堵塞和泄漏的情況比較多,關聯(lián)度較高。可見,關聯(lián)度較高是導致這三個子系統(tǒng)重要度較高的原因。在對數(shù)控磨床進行可靠性提升時,考慮到這三個子系統(tǒng)的重要度較高,應視為重點子系統(tǒng)優(yōu)先進行可靠性優(yōu)化。
頭( 尾) 架系統(tǒng)、基礎部件和主軸系統(tǒng)重要度排在4 到6 位,但差距不大。在對數(shù)控磨床進行可靠性提升時,應綜合考慮其他因素來確定需要優(yōu)先提升的子系統(tǒng)。量儀系統(tǒng)、冷卻系統(tǒng)和潤滑系統(tǒng)重要度較低,不作為優(yōu)先提升可靠性的子系統(tǒng)。
6、 總結
本方法考慮了各個子系統(tǒng)之間的關聯(lián)度,并弱化了評價的主觀影響,簡單易行,易于通過編程實現(xiàn)計算。通過實例證明該方法可以有效的對數(shù)控磨床系統(tǒng)進行了子系統(tǒng)的重要度評價,為制定數(shù)控磨床可靠性提升的決策路線提供了依據(jù),能夠更加有針對性的對各個子系統(tǒng)進行可靠性改進,進而更有效的提升整機可靠性。事實證明,該方法對數(shù)控磨床可靠性提升有著十分重要的指導意義。
如果您有機床行業(yè)、企業(yè)相關新聞稿件發(fā)表,或進行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com
- 2025年7月 新能源汽車銷量情況
- 2025年7月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年7月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年7月 軸承出口情況
- 2025年7月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年7月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年6月 新能源汽車銷量情況
- 2025年6月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年6月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年6月 軸承出口情況
- 2025年6月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年6月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年5月 新能源汽車銷量情況




