工業機器人位姿誤差空間 IDSW 插值補償方法研究
2017-7-11 來源:江蘇無錫 作者:陳宵燕 張秋菊 孫沂琳 陳海衛
在焊接、激光切割、自動化裝配等實際生產和應用中,機器人精度是衡量其性能的重要指標[1]。 一般而言,工業機器人具有較高的重復定位精度,而絕對定位精度較差,前者可達到0.1 mm人,而后者一般2~3 mm,無法滿足某些行業的生產要求。
目前提高絕對定位精度的方法主要分為兩種[2]:誤差預防法和誤差補償法。 前者主要是通過提高機器人設計和加工精度,這種方法不僅成本高而且不易實現。 后者也可稱為機器人標定,該方法通過使用先進的測量技術并且成功辨識出所建機器人模型中各項參數的準確值,然后通過修改機器人控制器中的參數或者增加一定的控制算法以達到提高定位精度的目的。 機器人標定是離線編程技術實用化的關鍵技術之一,其最后一步且關鍵一步為誤差補償[3],現階段誤差補償方法主要分為:基于模型的方法[4-7]和基于插補的方法[8-9]。
基于模型的補償方法的基本原理是:在假設主要誤差源為關節軸傾斜和關節偏移等幾何誤差的情況下,用機器人運動學模型來描述機器人位姿誤差。校準中要進行機器人模型參數對測量姿態誤差的擬合,用校準后的機器人模型預測各個位姿的誤差。基于模型的補償方法主要分為兩種[10]:
1) 關節空間補償。 利用標定后的結果直接在關節空間修正,對于某可達位姿,重新計算其關節值,來達到提高機器人位姿精度的目的;
2) 微分誤差補償。該方法一般是針對基于微分變換思想建立機器人誤差模型,識別幾何參數名義值與真實值之間的微小偏差,并把其補償控制器的名義參數上,達到提高機器人精度的目的。
基于模型的方法缺點是需建立復雜的運動學誤差模型,并需修改各項運動學參數從而造成機器人運動學逆解的困難,計算復雜且難以實現。
對于基于插補思想的誤差補償法,需要對機器人末端在機器人工作空間中的特定網格點的位姿進行測量,目前多數采用在工作空間用雙線性插補和多項式擬合等插補技術來擬合相應于不同定位誤差的關節補償指令。 此外,文獻[9] 提出一種空間插值法,該方法在前期將機器人工作空間劃分成的網格,對網格點進行位置誤差測量,然后采用空間插值來補償定位誤差。 但這種方法存在很多缺陷,目前只在沒有考慮姿態變化對位置誤差的影響下對位置誤差進行了補償,且沒有對姿態誤差進行補償,因此存在很大的局限性。
隨著高精度測量工具的不斷發展及普及應用,如FARO 激光跟蹤儀、LEICA 激光跟蹤儀等,使得基于插補的補償方法變得更為便捷、可靠,同時,完善并優化基于插補的補償方法也變得更為重要和緊迫。 針對空間插值補償方法,對機器人位姿誤差與其末端位置之間相關性進行探討,提出基于均勻數據場的空間IDSW 插值算法的機器人位姿誤差補償方法,并設計對比試驗,利用 MATLAB 進行仿真,結果證明該方法對機器人位姿精度提高的有效性。
1.機器人運動學誤差模型
DH 模型常用來對機器人空間的位姿進行表示和建模,這個建模方法由 Denavit 和 Hartenberg 兩人創新性提出的。 該建模方法優點在于其非常簡單且通用性非常好,可對任何構型的機器人的連桿和關節進行建模,方法為
Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(xi,αi) (1)
對于六自由度的串聯機器人,其末端的位置和姿態的坐標變換為

經典的 DH 模型存在參數不連續的缺點:假如相鄰關節軸線實際上不平行而理論上卻以平行來建模,則這兩個軸線間的相對位置誤差的建模將不能滿足“小誤差建模” 條件,造成參數突變。 “小誤差模型”定義如下:對于連桿坐標變換的微小位姿誤差能通過連桿參數的微小偏差對其進行建模[11]。
為了解決這種問題,Hayati 等[12]在經典 DH 運動學模型的基礎上,增加了一個新的繞y 軸的旋轉參數 βi,該模型被稱之為 MDH 模型。 該模型的相鄰連桿坐標變換的數學表達式為
Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(xi,αi)Rot(yi,βi) (3)
機器人定位精度誤差大體可以分為兩類:運動學(幾何)參數誤差和動力學(非幾何)參數誤差,具體包括幾何參數的偏差、關節偏移、連桿和關節的柔性、齒輪系結構、齒輪間隙、環境溫度等等。 運動學參數誤差主要由制造和裝配的誤差造成的,所導致的誤差占總誤差的 80%左右[13]。 所建立的機器人運動學誤差模型,主要考慮運動學參數誤差對機器人位姿誤差的影響。 除了以上運動學參數存在的誤差,在建立位姿誤差模型時,測量機器人末端實際位姿將引入機器人基坐標系相對于機器人構造的基坐標系之間的誤差 Δσ。 采用微分法[11]建立機器人運動學誤差模型,對式(3)進行全微分,得
dAi=∂ANi∂θiΔθi+∂ANi∂diΔdi+∂ANi∂aiΔai+∂ANi∂αiΔαi+∂ANi∂βiΔβi ( 4 )
式中: Δθi、Δdi、Δαi、Δai、Δβi分別表示連桿長度偏差、連桿偏置、扭角偏差、關節角偏差和相鄰平行軸的角度偏差。
由于該方法較成熟,在此對過程不做贅述,具體可參見文獻[11],最終所建立的運動學誤差模型為
E = J·ε(5)
式中:E 為位姿誤差;J 為辨識雅克比矩陣;ε 為運動學參數誤差。

2 定位位姿誤差模型
2.1 機器人位姿誤差與末端位置相關性
空間插值是指通過已知的數據點或已知的已劃為各個相對小一些的區域內的數據點,計算出相關的其他未知點或相關區域內的任意點的方法[14]。 研究的空間IDSW 插值補償法是基于笛卡爾坐標系下的空間插值,即選擇一定數量的機器人末端位置作為測量點,測量這些點所對應的位姿誤差,根據這些已知點所對應的位姿誤差來計算相關區域內其它任意位置的位姿誤差。 由此可知,機器人位置和機器人位姿誤差兩者之間的高相關程度是本文插值補償法有效的先決條件。
Pearson 相關(也稱為積差相關或積矩相關) 是英國統計學家皮爾遜于 20 世紀提出的一種計算直線相關的方法。 Pearson 相關系數用來衡量兩個數據集合是否在一條線上面。 其計算公式為
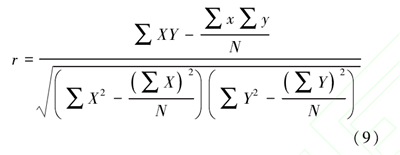
式中相關系數 r 的值介于-1 與+1 之間。
相關系數性質如下:
1) 當r >0 時,表示兩變量正相關,r <0 時,兩變量為負相關;
2) 當| r | =1 時,表示兩變量為完全線性相關,即為函數關系;
3) 當r =0 時,表示兩變量間無線性相關關系。
一般可按三級劃分:| r | <0.4 為低度線性相關;0.4 ≤| r | <0.7 為顯著性相關;0.7 ≤| r |<1 為高度線性相關。 低度線性相關又 可 分為 弱 相 關(0.2~0.4)和極弱相關或無相關(0.0~0.2)。
利用 Pearson 相關系數來衡量機器人位置和機器人位姿誤差之間的相關性程度。以 Staubli TX60L機器人為例,根據第 1 節所述方法建立運動學誤差模型,可知機器人的位置誤差和姿態誤差都是機器人關節角 θi的函數,由于姿態誤差數量級較位置誤差小,所以將位姿誤差分為位置誤差和姿態誤差,并分別進行分析。
利用 MATLAB 仿真功能,設計實驗 1,其步驟如下:
1) Staubli TX60L 機器人名義運動參數及設定的運動參數偏差值如表 1 所示,利用蒙特卡洛法隨機選取 101 組 6 個關節角度值,記錄其所對應的101 組機器人末端位置值。
表 1 Staubli TX60L 機器人運動參數名義值和偏差值

2) 將這 101 組關節值代入式(5),計算其對應的位置誤差 dΔ和位姿誤差 δΔ。
3) 計算第 1 組數據所對應的位置誤差dΔ和位置值分別與其它 100 組對應的置誤差dΔ和末端位置值的位置誤差差值 ΔdΔ和位置值差值 dz,利用MATLAB 得到 ΔdΔ和 dz的兩者的相關性(用散點圖表示,見圖 1)和 Pearson 相關系數r1;

圖 1 兩點的位置誤差差值與dz相關性
4) 計算第 1 組數據所對應的姿態誤差δΔ和位置值分別與其它 100 組對應的位姿誤差δΔ和末端位置值的姿態誤差差值 ΔδΔ和位置值差值 dz,利用MATLAB 得到 ΔδΔ和 dz的兩者之間的相關性(用散點圖表示,見圖 2)和 Pearson 相關系數r2;
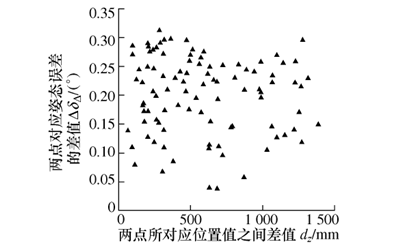
圖 2 兩點的姿態誤差差值與dz相關性
利用 MATLAB 計算得到 ΔdΔ和 dz的 Pearson 相關系數 r1= 0.015 7, ΔδΔ和 dz的 Pearson 相關系數r2= -0.079 2。 圖 1 所描述的兩點所對應的位置誤差之間的差值與位置值間的差值不具有明顯的關系,根據計算所得相關系數r1可知兩變量的線性關系幾乎為無相關。 圖 2 所示兩點所對應的姿態誤差之間的差值與位置值間的差值也不具有明顯關系,同時根據所得的相關系數r2可知其線性關系也幾乎為無相關。 而對機器人來說,末端執行器的位姿由位置和姿態共同決定,所以在研究機器人位置和機器人位姿誤差兩者之間的相關性時,存在一個可控變量———姿態。 因此,設計實驗 2,其步驟如下:
1) 利用蒙特卡洛法選取 Staubli TX60L 機器人工作空間 101 組機器人末端位置值,記錄其所對應的101 組機器人位置值,任意選取某一姿態,在該姿態下,對上述 101 個位置經運動學逆解得到 101 組6 個關節角度值;
2) 同實驗 1 的步驟 2);
3) 同實驗 1 的步驟 3),亦利用 MATLAB 得到ΔdΔ和 dz的兩者之間的相關性(用散點圖表示,見圖3 所示)和 Pearson 相關系數r3;

圖 3 兩點的位置誤差差值與dz相關性
4) 同實驗 1 的步驟 4),亦利用 MATLAB 得到ΔδΔ和 dz的兩者之間的關系圖(用散點圖表示,如圖4 所示)和 Pearson 相關系數r4。
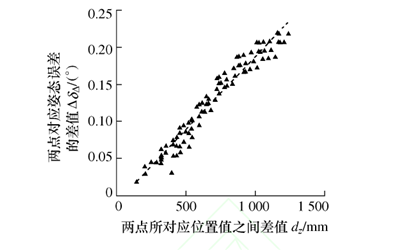
圖 4 兩點的姿態誤差差值與dz相關性
利用 MATLAB 計算得到 ΔdΔ和 dz的 Pearson 相關系數 r3為 0.73,ΔδΔ和 dz的 Pearson 相關系數r4為 0.98。 比較圖 1 和圖 3,并根據所求的相關系數r1和 r3,可知通過控制機器人末端姿態這一變量后,兩點對應的位置誤差間的差值與位置值間的差值之間呈高度線性相關;分析比較圖 2 和圖 4,并根據所求的相關系數 r2和 r4,可知在機器人末端姿態不變的情況下,兩點對應的姿態誤差間的差值與位置值間的差值之間呈高度線性相關。 綜上所述,在機器人的工作空間內,若機器人末端姿態保持一致,則兩點所對應的位置值的差值 dz越大,所對應的位置誤差差值 ΔdΔ和姿態誤差差值 ΔδΔ也越大,且兩者關系均呈高度線性相關。 而此時,所提出的空間 IDSW插值補償法對機器人位姿誤差補償有效的前提條件成立。
2.2 姿態變化因素下的定位位姿誤差模型
根據 2.1 節的結論可知,為使空間 IDSW 插值補償方法能對機器人位姿誤差補償在任意姿態下均有效,必須考慮姿態變化對位姿誤差的影響。 所以將重點研究如何建立固定位置時姿態變化因素下的定位位姿誤差模型。
機器人運動姿態的有兩種常用描述方法:機械人末端的運動方向和繞軸 x,y,z 的旋轉序列(歐拉角)。 前者是關于機器人運動學模型計算得到接近矢量 a,方向矢量n,法線矢量o,即式(2) 機器人末端坐標系變換矩陣的旋轉矩陣對應的 3 個列矢量;后者是笛卡爾坐標空間下,對機器人位置控制時運動姿態的 3 個重要參數,一般工業機器人的姿態表示法采用的是 x_y_z 歐拉角,即歐拉角Φ,θ,φ。 這種描述在基坐標系{B} 的方位的法則如下:基坐標系{B} 與參考系{A} 相同,首先使{B} 繞xB軸轉 Φ 角,然后繞yB軸轉 θ 角,最后繞zB軸轉 φ 角,如圖 5 所示。
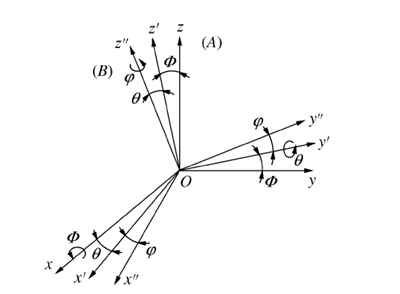
圖 5 x?y?z 歐拉角法則
根據右乘的原則,可以求得與之等價的旋轉矩陣,即(圖片)
由此可知,給定x-y-z 歐拉角 Φ,θ,φ, 便可確定對應的旋轉矩陣。當給定旋轉矩陣,也可求出等價的x-y-z 歐拉角Φ,θ,φ。 令

由上述可知,繞zB軸轉 φ 角只影響方向矢量 n和法線矢量 o,與接近矢量a 無關,同時經研究可知旋轉角 φ 對位姿誤差的影響呈三角函數關系。 因此,對固定位置時姿態變化的定位位姿誤差模型確立分為兩步:正弦函數相位角偏移誤差建模和矢量夾角加權平均誤差建模。

圖 6 定位下所選取的 9 個姿態
首先對機器人姿態操作空間以接近矢量劃分,令 φ =0 只考慮歐拉角 Φ 和 θ,選取 9 個具有代表性的姿態,如圖 6 所示。 其次就是考慮歐拉角φ 對機器人位姿誤差的影響,對以上9 個姿態分別測量3 個不同歐拉角 φ 時的位姿誤差,建立正弦函數,即
A = B*sin(φ - w)- C (12)
由此得到任意歐拉角φ時這9個姿態所對應的位姿誤差,這就是正弦函數相位角偏移誤差。
對機器人的其他操作姿態所對應的位姿誤差可利用矢量夾角加權平均求得。 根據如圖 6 所示的已知 9 個姿態的每個姿態均有相對應的接近矢量、方向矢量和法線矢量,與所求姿態所對應的接近矢量、方向矢量和法線矢量分別進行夾角算,選取夾角量最小的 3個姿態并根據第一步獲得該 3 個姿態對應的位姿誤差來進行量夾角加權平均計算,得到該姿態下的位姿誤差。 綜合上述兩步,就是建立的在姿態變化因素下的定位位姿誤差模型為
E′ =∑3i =1E(i)× λi ( 1 3 )
式中:E(i) 為 9個代表性姿態經第一步獲得所求姿態下對應的位姿誤差;λi為矢量夾角加權值。
3 空間IDSW 插值補償模型
對機器人位姿誤差補償是基于空間插值法,空間插值方法很多。 依據空間插值的基本假設和數學本質可分類為:幾何方、統計方法、空間統計方法、函數方法、隨機模擬方法、物理模型模擬方法和綜合方法[15]。 幾何方法包括反距離加權法、泰森多邊形法等;統計方法包括趨勢面、多元回歸法和多面函數法等;空間統計方法包括克里金法、最小二乘配置和楊赤中法等;函數方法包括樣條函數、雙線性內插方法[16]。 所提出的空間 IDSW 插值補償法選擇的是反距離加權法來進行機器人位姿誤差插值補償,該算法是以距離作為權重的滑動平均加權插值法[17],它是根據離散點生成規則網格數據最常見的空間內插方法,計算過程簡單且運算速度快。
根據第 2.1 節的研究結果可知,當機器人末端姿態一致時,其末端任意兩點所對應的位置誤差間的差值 ΔdΔ和姿態誤差間的差值 ΔδΔ分別與該兩點位置間的差值 dz具有高度的線性相關性。 根據第2.2 節所建立的定位位姿誤差模型,可以將所測量點(即已知點) 的姿態所對應的位姿誤差轉換到需要預測的位姿的姿態所對應的位姿誤差,使得機器人末端姿態保持一致的條件成立,滿足了第 2.1 節所提出的空間插值補償法有效性的先決條件,從而為空間 IDSW 插值算法在機器人位姿誤差補償上奠定了理論基礎和應用基礎。
根據采集點的分布可以采集數據分為規則采集點數據集點和離散采集點數據集。 前者可使反距離加權算法具有更好的逼近程度,本文將對機器人操作空間的規則采集點數據集稱為均勻數據場。 因此,將機器人的工作空間劃分為均勻網格,而對于某一目標點 M,使用快速搜索法得到距離M 點最近的8 個包絡點,如圖 7 所示。
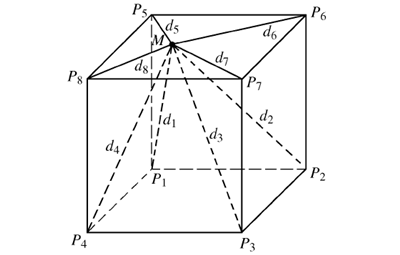
圖 7 基于反距離加權算法的位姿補償原理
利用反距離加權法[18-19],可得位置誤差和姿態誤差的補償模型為:
d∗Δ=∑8i =1dΔ(i)× ρi(14)
δ∗Δ=∑8i =1δΔ(i)× ρi(15 )
式中:d*Δ和 δ*Δ為目標點的預測位置誤差和姿態誤差;dΔ(i)和δΔ(i)為目標點周圍 8 個包絡點的位置誤差和姿態誤差;ρi為 8 個包絡點的權重,權重的公式為
ρi=1dki∑8j =11dkj(16)
式中:di或 dj為目標點與周圍 8 個包絡點之間的距離;k 為冪指數。
在式(16)中,k 值越大,插補結果越具有平滑,當取 k= 2 時, 通常稱為反距離 平 方 加 權 ( 簡 稱IDSW)算法。 因此,在基于空間插值的反距離平方加權算法下,提出機器人位姿誤差空間 IDSW 插值補償方法,上述所建立的補償模型即為基于均勻數據場的空間 IDSW 插值補償模型。
4 仿真驗證
為驗證空間 IDSW 插值算法對機器人位姿誤差補償的有效性,將利用目前較為成熟的微分誤差補償法與本文所提出的方法進行對比試驗。 微分誤差補償法即基于位姿誤差模型,將辨識得到的參數偏差來修正名義參數,來達到誤差補償效果。
在本文第 2 節中,以 Staubli TX60L 機器人為例已建立了運動學位姿誤差模型,然后對辨識雅克比矩陣進行 QR 分解,剔除兩個無法辨識的參數:dZB和 δZB, 再使用最小二乘法對其余 28 個參數進行辨識,結果如表 2 所示。 最后將該辨識得到的參數偏差用于基于微分誤差補償法補償實驗。
表 2 最小二乘法參數辨識結果

基于空間 IDSW 插值算法的機器人位姿誤差補償方法首先需要建立合適的空間網格,將 StaubliTX60L 機器人的某局部工作空間劃分為均勻網格,令網格邊長為 100 mm,以機器人末端的笛卡爾坐標系來劃分,X 軸向工作范圍為(300 mm~500 mm),Y軸向工作范圍為( -400 mm ~ 400 mm),Z 軸向工作范圍為( -100 mm ~ 200 mm),具有 48 個網格,108個網格頂點。仿真實驗如下:利用 MATLAB 建立基于 MDH模型的 Staubli TX60L 機器人運動學模型,并編寫空間 IDSW 插值算法和遞歸搜索算法;選取 3 個不同姿態,分別在這 3 個姿態下,在網格空間中任取 3 個點,共 9 個選取的驗證點如表 3 所示。 利用表 1 預定義的運動參數的偏差值,修改運動學模型的參數,分別計算這 9 個點所對應的位置誤差和姿態誤差,結果分別見圖 8和圖 9。
表 3 選取的驗證點
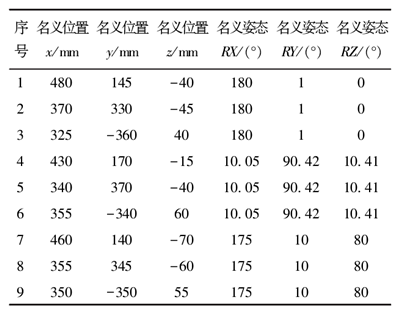
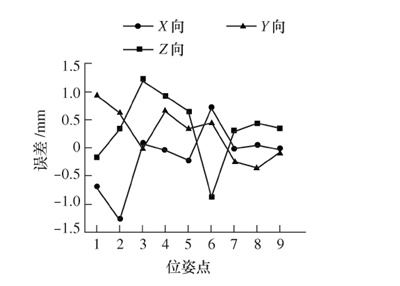
圖 8 補償前位置誤差

圖 9 補償前姿態誤差
分別計算 108 網格頂點在如上 3 個姿態下所對應的位置誤差和姿態誤差,所得誤為采集點數據集,用以建立空間 IDSW 插值算法所需的均勻數據場;分別根據微分誤差補償法(圖中簡稱微補法)和空間 IDSW 插值算法(圖中簡稱 IDSW 法)對機器人位姿誤差進行補償,其結果如圖 10 和圖 11 所示。

圖 10 微補法和 IDSW 法補償后的位置誤差 1 和 2

圖 11 微補法和 IDSW 法補償后的姿態誤差 1 和 2
根據 MATLAB 仿真實驗結果,在 3 個不同姿態下, 微 分 誤 差 補 償 法 補 償 后 位 置 精 度 平 均 提84.8%,83.1%,59.4%,姿態精度平提高 95.9%,96.6%,94.6%;而經反距離平方比加權算法補償后位置精度平均提高 98.0%,98.5%,93.5%,姿態精度平均提高 98.7%,98.5%,97.3%。 所以采用微分誤差補償法和空間 IDSW 插值算法對位姿誤差都具有較好的補償效果。 分析圖 10 和圖 11 可知,空間IDSW 插值算法對位置補償效果優于微分誤差補償法,同時姿態補償效果也優于微分誤差補償法。 因此,所提出的補償方法補償效果更好,且不需要建立復雜的機器人位姿誤差模型,不需要進行繁瑣的參數辨識過程。 綜上所述,經 MATLAB 的對比實驗仿真驗證,在只考慮運動學參數偏差引起的位姿誤差情況下,所提出的插值算法對機器人位姿誤差補償是有效的。
5 結論
在探討機器人誤差補償的現有方法之上,研究基于空間插值的補償方法,并提出機器人末端位置與機器人末端位姿誤差的相關性程度是決定插補補償方法是否有效的充分條件。 首先利用 Staubli TX60L 的DH 參數建立運動學模型,并預定義各項運動參數的偏差值,使用 MATLAB 建模仿真分析,得到當機器人末端姿態不變時,任意兩點對應的位置誤差之間的差值和姿態誤差之間的差值分別與兩點間的位置差值具有高度線性關系。 然而機器人末端任意姿態時,兩點的位置誤差的差值和姿態誤差的差值分別與兩點間的位置差值之間幾乎無關。 因此,提出了一種姿態變化因素下的定位位姿誤差模型。 最終提出機器人位姿誤差空間 IDSW 插值補償方法,并由 MATLAB 仿真驗證了該補償方法的有效性。
所提出的位姿誤差補償方法最大的優點是不需要建立機器人位姿誤差模型,也不需要辨識機器人復雜、冗余的各項參數,在測量上也只需要有限的采集點,尤其是對在機器人操作時末端執行器具有任意姿態且對姿態要求高的機器人應用領域具有較好的應用前景,
該方法具有計算過程簡單、速度快、補償效果好等優點。 基于空間 IDSW 插值算法是一種空間內插方法,只能對網格空間內的數據進行補償,所以需探索擴展方法,研究具有外推能力的插值方法將是后續的研究工作。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





