基于全微分模型的打磨機械臂靜態(tài)誤差分析
2017-1-3 來源: 東北大學(xué)機械工程及自動化學(xué)院 作者:張秀珩 柳洪義 巴鵬
摘要: 針對打磨機械臂系統(tǒng)的精度設(shè)計問題的解決, 基于DH 模型建立了機械臂的運動學(xué)參數(shù)模型, 并基于全微分法建立了運動學(xué)參數(shù)誤差與末端誤差的數(shù)學(xué)關(guān)系。對機械臂可能出現(xiàn)的誤差源進行分析, 歸納誤差源的類型, 代入誤差模型分別進行仿真, 并對結(jié)構(gòu)誤差與傳動誤差對機械臂末端位置的影響進行比較。結(jié)果表明: 傳動誤差對X、Y 向的位置影響較大, 而結(jié)構(gòu)誤差對Z 軸的影響較大, 這些信息可用于對實際機械臂參數(shù)誤差的回歸分析, 為在機械臂設(shè)計及制造階段、機械臂的制造及裝配誤差預(yù)計及優(yōu)化提供數(shù)據(jù)參考。
關(guān)鍵詞: 打磨機械臂; 全微分; 靜態(tài)誤差; 誤差分析
0.前言
大多數(shù)的工業(yè)用機械臂, 其末端執(zhí)行器的位姿精度是衡量其工作性能的重要指標(biāo)。對機械臂進行運動學(xué)標(biāo)定是目前提高機械臂靜態(tài)精度最有效的方法, 最普遍的做法是首先建立機械臂的正運動學(xué)模型, 既而建立相關(guān)的位姿誤差模型, 通過識別機械臂末端位姿與各運動學(xué)參數(shù)之間的關(guān)系來實現(xiàn)誤差優(yōu)化, 從而達(dá)到提高位姿精度的目的。在實際應(yīng)用中, 該方法可大幅提高機械臂的靜態(tài)精度, 但由于各種機械臂在結(jié)構(gòu)和功能上的差別, 其各單項原始輸入誤差對末端位姿誤差的影響必然不同[1] , 所以對影響位姿誤差的誤差源的分析及在設(shè)計階段對機械結(jié)構(gòu)的改進也尤為重要。
影響機械臂靜態(tài)誤差的因素主要有幾何誤差(靜態(tài)誤差)、因動態(tài)載荷及機體振動引起的動態(tài)誤差、因溫度影響引起的誤差及環(huán)境、控制系統(tǒng)和算法誤差[2] 。IMOTO J 等[3] 研究了幾何誤差、溫度變化等因素對機械臂定位精度的影響。SANTOLARIA J 等[4]為優(yōu)化機械臂運動學(xué)標(biāo)定條件, 基于輸出姿勢誤差和測量誤差的線性關(guān)系, 給出一種在標(biāo)定后用于估計輸出姿態(tài)誤差和誤差評價指標(biāo)的方法。ZHUANG H等[5] 基于Monte Carlo 方法, 提出在機械臂標(biāo)定過程中采用圓點分析法評估標(biāo)定標(biāo)定結(jié)果的不確定性。在機械臂標(biāo)定方法的研究發(fā)展了多種測量方法, 如HOLLERBACH J M 等[6] 通過在機械臂末端執(zhí)行器上加運動約束, 使機械臂末端保持固定的閉環(huán)標(biāo)定方法。IKITS M 等[7] 通過確定機械臂的各關(guān)節(jié)軸線位置, 解析各旋轉(zhuǎn)軸之間的代數(shù)關(guān)系并確定運動學(xué)參數(shù)。KHALIL W 等[8] 采用極坐標(biāo)法研究多約束激光跟蹤系統(tǒng)運動目標(biāo)標(biāo)定。
本文作者根據(jù)實際工程項目需求, 對課題組研制開發(fā)的發(fā)動機絕熱層機械打磨機械臂的靜態(tài)精度進行研究, 為保證打磨精度, 首先對機械臂的靜態(tài)精度有重要影響的因素進行分析, 確定靜態(tài)誤差的靈敏度, 再針對機械臂的末端位置及姿態(tài)精度進行標(biāo)定。
1.打磨機械臂運動學(xué)建模
為獲得打磨機械臂運動學(xué)模型, 采用D-H 方法建模。根據(jù)機械臂的機械構(gòu)型, 對機械臂主體部分進行簡化, 選取本體質(zhì)心處, 建立基坐標(biāo)系SB , 大臂底座中心建立坐標(biāo)系S1 , 并依次建立各關(guān)節(jié)坐標(biāo)系和末端坐標(biāo)系S e 。關(guān)節(jié)1、2、3對應(yīng)的變量分別記為d , θ2, θ3,桿件1 、 2、 3 的長度分別記為 l、1 l 2、 l3。用D-H (Denavt-Hartenberg) 法建立各坐標(biāo)系模型。根據(jù)文中所研究的打磨機械臂幾何結(jié)構(gòu)及運動參數(shù)分別如圖1 和表1 所示。
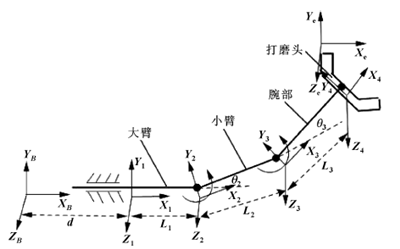
圖1 機械臂各關(guān)節(jié)的運動學(xué)參數(shù)及坐標(biāo)系
表1 D-H 參數(shù)表
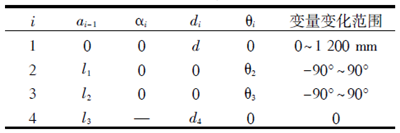
根據(jù)表1 所示機械臂參數(shù)可確定運動學(xué)模型如下:

2.打磨機械臂誤差建模
采用全微分的方法對式(1) 進行微分, 即可得到


為了描述末端位姿誤差與各幾何誤差源之間的關(guān)系, 采用矩陣的形式建立串聯(lián)機構(gòu)的幾何誤差模型為:


3.打磨機械臂靜態(tài)誤差分析
為完成機械臂標(biāo)定并正確評價機械臂的性能, 誤差模型的建立首先應(yīng)從了解其誤差源入手。當(dāng)忽略控制算法誤差的影響后, 根據(jù)誤差的性質(zhì)和來源來看,主要包括靜態(tài)誤差和動態(tài)誤差。其中靜態(tài)誤差包括由于機械臂本體的制造和裝配過程中產(chǎn)生的幾何參數(shù)誤差, 還有因環(huán)境(如溫度)、傳動誤差及因重力等引起的變形誤差, 與幾何參數(shù)誤差相比, 這部分誤差所占比重較小。動態(tài)誤差主要指機械臂在工作過程中因力矩、摩擦力、振動等原因隨時間變化的誤差。在這諸多的影響因素中, 幾何參數(shù)誤差是影響機械臂精度的最重要的因素, 因此主要針對這一誤差加以分析。
在影響機器人末端執(zhí)行器精度的主要因素中, 重點考慮結(jié)構(gòu)誤差、傳動誤差、關(guān)節(jié)間隙與連桿機構(gòu)的撓性。對于旋轉(zhuǎn)關(guān)節(jié), 隨著旋轉(zhuǎn)角的增大, 關(guān)節(jié)的旋轉(zhuǎn)誤差將累積增大, 而對本機器人來說由于其移動關(guān)節(jié)的采用直線導(dǎo)軌結(jié)構(gòu)且運動量程較長, 所以其直線度誤差不容忽視。因此在選擇誤差項時根據(jù)機器人的本體結(jié)構(gòu), 確定各連桿的長度誤差、直線度誤差、旋轉(zhuǎn)關(guān)節(jié)的垂直度誤差及各關(guān)節(jié)的運動參數(shù)誤差作為主要誤差源, 其誤差項的取值及極限范圍如下:

對本機械臂來說, 其末端的位置精度是影響其工作性能的主要因素, 所以這里僅對機器人的末端位置誤差進行分析, 機械臂在實際工況中執(zhí)行兩個動作,一個是僅大臂直線的移動動作; 一個是3 個關(guān)節(jié)都運動的曲線動作, 針對各單項誤差分別對兩種動作時的誤差進行仿真, 可得到關(guān)節(jié)誤差、結(jié)構(gòu)誤差與末端位置誤差的關(guān)系曲線如圖2—7 所示。(1) 當(dāng)僅考慮連桿長度誤差時, 軌跡1 和軌跡2的末端誤差與連桿長度誤差之間的關(guān)系如圖2 和3所示。
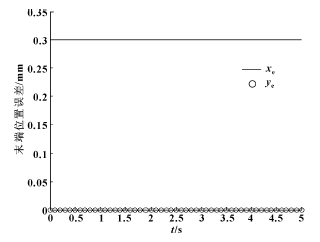
圖2 沿軌跡1 運動時末端的位置誤差分布
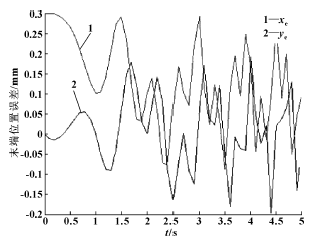
圖3 沿軌跡2 運動時末端的位置誤差分布
由圖可以看出, 對軌跡1, 當(dāng)僅移動關(guān)節(jié)運動時, 連桿誤差僅對末端X 軸方向位置精度有影響,且xe =0.3 mm; 對軌跡2 來說, 因3 個關(guān)節(jié)的共同運動產(chǎn)生的末端位置在X 和Y 2 個方向的位置精度都有影響, 從變化規(guī)律上看2 個方向的誤差變化相似,但在X 軸正向的影響明顯較大, 均值約為0.25 mm。
(2) 當(dāng)僅考慮因結(jié)構(gòu)參數(shù)誤差因素時, 軌跡1與軌跡2 的末端位置誤差表現(xiàn)如圖4 和5 所示。

圖4 沿軌跡1 運動時末端的位置誤差分布
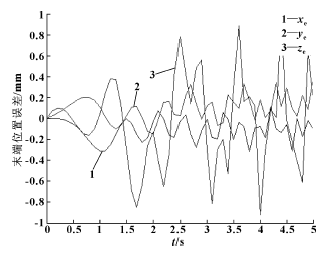
圖5 沿軌跡2 運動時末端的位置誤差分布
由圖可以看出, 當(dāng)僅考慮幾何誤差(形狀與位置誤差) 時, 對軌跡1, 末端位置在Y 軸方向位置誤差隨移動關(guān)節(jié)的運動而逐漸變大, X、Z 軸誤差則較小; 對第二段軌跡來說, 末端位置在3 個方向的誤差都較大, 其中在Z 向的誤差均值為0.6 mm, 且誤差呈周期性變化, X 和Y 向的誤差較小, 誤差均值為0.3 mm 左右。
(3) 僅考慮關(guān)節(jié)傳動誤差時, 末端位置精度與關(guān)節(jié)角誤差之間的關(guān)系如圖6 和7 所示。
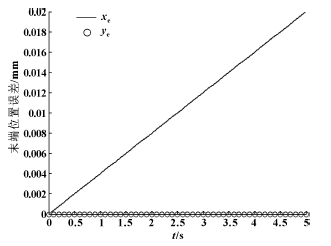
圖6 末端位置誤差與移動關(guān)節(jié)誤差的分布關(guān)系
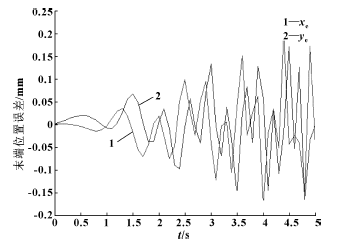
圖7 末端位置誤差與轉(zhuǎn)動關(guān)節(jié)誤差的分布關(guān)系
由圖6 可知, 僅考慮移動關(guān)節(jié)的傳動誤差時, 末端僅在X 向有誤差, 由于傳動誤差被定義為均勻分布, 所以該誤差大小與關(guān)節(jié)位移呈正比例, 在規(guī)定時間內(nèi)的位置誤差最大為0.02 mm; 由7 圖可知, 當(dāng)僅考慮關(guān)節(jié)角誤差時, 在X 和Y 向的末端位置均有誤差,且隨關(guān)節(jié)角的增加, 誤差呈周期性變化, 均值在0.2mm 左右。
為了分析結(jié)構(gòu)誤差和傳動誤差對機械臂末端的綜合影響, 分別令傳動誤差不變, 分析結(jié)構(gòu)誤差對機械臂末端的位置誤差的影響, 再令結(jié)構(gòu)誤差不變, 分析傳動誤差對機械臂末端的位置影響。由上圖可知, 機械臂的關(guān)節(jié)傳動誤差在X、Y 方向?qū)δ┒宋恢玫挠绊戄^大, 且呈周期性變化, 而因幾何誤差造成的結(jié)構(gòu)誤差則對Z 向的位置造成影響, 隨著誤差的變大, 末端位置誤差也增大, 成正比例關(guān)系, 這是由于末考慮誤差分布的影響。綜合來看, 轉(zhuǎn)角誤差引起的傳動誤差對末端的影響要小于結(jié)構(gòu)誤差的影響, 因此在誤差補償時應(yīng)多考慮Z 軸的誤差, 這是由機械臂的結(jié)構(gòu)所決定的。同時根據(jù)以上結(jié)果, 在機械臂的精度設(shè)計時也應(yīng)重要關(guān)注Z 向尺寸鏈的誤差控制。
4.結(jié)論
(1) 采用DH 模型法建立打磨機械臂的運動學(xué)參數(shù)模型, 并基于全微分法建立了運動學(xué)參數(shù)誤差與末端誤差的數(shù)學(xué)關(guān)系, 為后面進行誤差分析打好基礎(chǔ)。
(2) 對機械臂可能出現(xiàn)的誤差源進行分析, 歸納誤差源的類型, 代入誤差模型進行仿真, 得出結(jié)構(gòu)誤差與傳動誤差對機械臂末端位置的影響, 并根據(jù)仿真結(jié)果對誤差變化對末端位置的影響進行分析, 這些信息可用于對實際機械臂參數(shù)誤差的回歸分析, 為在機械臂設(shè)計及制造階段, 機械臂的制造及裝配誤差預(yù)計及優(yōu)化提供數(shù)據(jù)參考。
投稿箱:
如果您有機床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表,或進行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表,或進行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com
更多相關(guān)信息
業(yè)界視點
| 更多
行業(yè)數(shù)據(jù)
| 更多
- 2025年6月 新能源汽車銷量情況
- 2025年6月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年6月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年6月 軸承出口情況
- 2025年6月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年6月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年5月 新能源汽車銷量情況
- 2025年5月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年5月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年5月 軸承出口情況
- 2025年5月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年5月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年4月 新能源汽車銷量情況





